Pada awalnya sepeda tidak menggunakan rantai dan pedal, sehingga untuk menaikinya dilakukan dengan cara mendorong sepeda sampai berjalan dengan kakinya. Sepeda yang ada saat ini, umumnya mempunyai pedal yang dipasang pada rangka dan dihubungkan oleh sebuah rantai ke poros belakang. Ketika kalian mengayuh sepeda, kekuatan kaki kalian disalurkan ke roda belakang oleh rantai yang menghubungkan sepasang roda gir. Jika diameter kedua gir dan jarak pusat gir diketahui, dapatkah kalian menentukan panjang rantai?
Kunci jawaban latihan 3 matematika GARIS SINGGUNG LINGKARAN kelas 8
Latihan 3 halaman 93-94
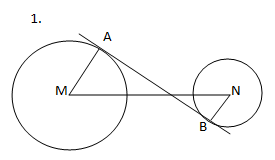
Pada gambar di atas, panjang jari-jari MA=7 cm, panjang jari-jari NB=5 cm, dan panjang MN=20 cm. Hitunglah panjang garis singgung persekutuan dalam AB
2. Panjang garis singgung persekutuan dalam dua lingkaran adalah 20 cm. Panjang jari-jari kedua lingkaran itu masing-masing adalah 9 cm dan 6 cm. Hitunglah jarak kedua pusat lingkaran tersebut
3. Panjang garis singgung persekutuan dalam dua lingkaran adalah 24 cm dan jarak kedua pusatnya adalah 26 cm. Panjang salah satu jari-jari lingkaran 7 cm. Hitunglah panjang jari-jari lingkaran yang lain
4. Jarak titik pusat dua lingkaran adalah 20 cm dan panjang garis singgung persekutuan dalamnya adalah 16 cm. Jika panjang jarr-jari lingkaran pertama adalah 2 kali panjang jari-jari lingkaran kedua, hitunglah panjang jari-jari lingkaran pertama
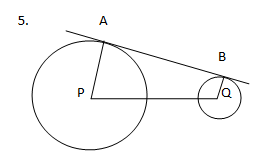
Pada gambar di atas, panjang jari-jari PA=12 cm, panjang jari-jari QB=5 cm, dan jarak PQ=25 cm. Hitunglah panjang garis singgung persekutuan luar AB
6. Panjang jari-jari dua buah lingkaran masing-msing adalah 21 cm dan 5 cm. Panjang garis singgung persekutuan luarnya adalah 30 cm. Hitunglah jarak kedua pusat lingkaran tersebut
7. Gambar berikut menunjukkan dua lingkaran yang saling bersinggungan
AB adalah garis singgung persekutuan luar, panjang AP=4 cm, dan panjang BQ=7 cm. Hitunglah panjang AB
8. Panjang garis singgung persekutuan luar dua lingkaran adalah 15 cm. Jarak kedua pusat lingkaran tersebut adalah 17 cm, dan panjang salah satu jari-jari lingkaran 3 cm. Hitunglah panjang jari-jari lingakran yang lain
9. Jarak titik pusat dua lingkaran adalah 15 cm dan panjang jari-jarinya masing-masing 7 cm dan 4 cm. Hitunglah panjang garis singgung berikut
a. Persekutuan dalam
b. Persekutuan luar
10. Panjang jari-jari dua buah lingkaran adalah 9 cm dan 3 cm. Panjang garis singgung persekutuan luanya adalah 1¼ kali panjang garis singgung persekutuan dalam. Hitunglah jarak kedua pusat lingkaran tersebut
11. Pada gambar beikut, gir belakang dan dapat sebuah sepeda motor dihubungkan dengan rantai yang melingkar pada kedua gir tersebut
JAWABAN
1. d²=p²-(r₁+r₂)²
d²=20²-(7+5)²
d²=20²-12²
d²=400-144
d²256
d=√256
d=16 cm
2. d²=p²-(r₁+r₂)²
20²=p²-(9+6)²
20²=p²-15²
400=p²-225
400+225=p²
625=p²
√625=p
25 cm=p
3. d²=p²-(r₁+r₂)²
24²=26²-(7+r)²
576=676-(7+r)²
576=676-47-r²
r²=676-47-576
r²=51
r=√51
r=7,1 cm
4. d²=p²-(r₁+r₂)²
16²=20²-(2r+r)²
256=400-(3r) ²
256=400-9r²
9r²=400-256
9r²=144
r²=144/9
r²=16
r=√16
r=4 cm
5. l²=p²-(r₁-r₂)²
l²=25²-(12-5) ²
l²=25²-7²
l²=625-49
l²=576
l=√576
l=24 cm
6. l²=p²-(r₁-r₂)²
30²=p)²-(21-5)²
30²=p²-16²
900=p²-256
900+256=p²
1156=p²
√1156=p
34 cm=p
7. p=AP+BQ= 4+7=11 cm
l²=p²-(r₁-r₂)²
l²=11²-(7-4)
l²=11²-3²
l²=121-9
l²=112
l=√112
l=10,6 cm
8. l²=p²-(r₁-r₂)²
15²=17²-(3-r) ²
225=289-(9+r²)
225=289-9-r²
225=280-r²
r²=280-225
r²=55
r=√55
r=7,4 cm
9. a. d²=p²-(r₁+r₂)²
d²=15²-(7+4)²
d²=15²-11²
d²=225-121
d²=104
d=√104
d=10,2 cm
b. l²=p²-(r₁-r₂)²
l²=15²-(7-4)²
l²=15²-3²
l²=225-9
l²=216
l=√216
l=14,7 cm
10. l²=p²-(r₁-r₂)²
(1¼d)²=p²-(9-3) ²
((5/4)d)²=p²-6²
(25/16)d²=p²-36
(25/16)d+36=p²
√(25/16)d²+36=p
(5/4)d+6=p
11. l²=p²-(r₁-r₂)²
l²=42²-(24-12)²
l²=42²-12²
l²=1764-144
l²=1620
l=√1620
l=40,2 cm
Demikianlah soal dan kunci jawaban latihan 3 dari materi bab 8 garis singgung lingkaran di semester 2. Agar bisa memahami matematika maka perbanyaklah mengerjakan contoh soal. Ingatlah untuk mengingat dua rumus garis isnggung lingkaran di atas. Untuk para pembaca terima kasih, dan Silahkan berikan komentar serta saran yang positif.
Sumber buku: Matematika untuk SMP/MTs kelas viii semester 2 kurikulum 2013 revisi. Penerbit Erlangga




Post a Comment