Teorema Pythagoras menyatakan bahwa pada suatu segitiga siku-siku, luas persegi pada sisi miring sama dengan jumlah luas persegi pada sisi-sisi lainnya. Teorema tersebut membantu manusia dalam banyak bidang. Pada bidang arsitektur. Teorema ini digunakan untuk merancang konstruksi bangunan. Misalnya menghitung panjang rangka kuda-kuda yang berbentuk segitiga siku-siku. Dapatkah kamu menhitung panjang kayu yang dibutuhkan untuk membuat rangka kuda-kuda?
Kunci jawaban Matematika latihan 3 TEOREMA PYTHAGORAS kelas 8
1. Dari tiga-tigaan bilangan berikut, manakah yang dapat membentuk segitiga siku-siku, lancip, atau tumpul?
a. 9, 6, 11
b. 7,10,12
c. 12,16,20
d. 8,11,13
e. 9,14,17
f. 2,5,√29
g. 7,12,14
h. 7,5;4;8,5
2. Dagi tiga-tigaan bilanagan berikut, manakah yang merupakan tripel Phytagoras?
a. 7,13,9
b. 8,15,17
c. 29,20,21
d. 6,2½,6½
e. 13,5,12
f. 24,17,25
g. 12,37,35
h. 9,5,√34
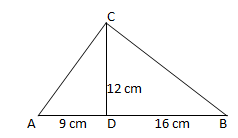
3. Perhatikan gambar berikut!
a. Hitunglah panjang AC!
b. Hitunglah panjang BC!
c. Berdasarkan kebalikan teorema Pythagoras, buktikan bahwa segitiga ACB siku-siku!
4. Perhatiakan gambar berikut!
Pada segitiga PQR di atas, panjang RS=4 cm, PS=8 cm, dan QS=16 cm.
a. Hitunglah panjag PQ!
b. Hitunglah panjang PR!
c. Tunjukkan bahwa segitiga PQR siku-siku di P!
5. Gambar berikut adalah limas P.ABC dengan alas segitiga ABC yang siku-siku di C. PC tegak lurus dengan CA dan PC tegak lurus dengan CB. Panjang AC=24 cm, bc=10 cm, dan PC=18 cm.
b. Tentukan jenis segitiga ABP (segitiga lancip, tumpul, atau siku-siku)!
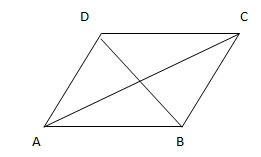
6. Pada segi empat ABCD berikut, panjang diagonal AC=30 cm, BD= 16 cm, dan panjang sisi AD=17 cm.
a. Buktikan bahwa diagonal AC dan BD berpotongan tegak lurus!
b. Berbentuk bangun apakah ABCD!
b. Sudut manakah yang merupakan sudut siku-siku?
b. Berbentuk bangun apakah ABCD!
7. Mita (M) berada di atas balkon rumahnya. Di kejahuan, ia melihat Katrin (K) yang berjarak 7 m dari bawah balkon tempat Mita berdiri, kemudian ia melihat Lusi (L) yang berada dekat pagar rumah dan berjarak 3 m dari tempat yang sama. Tinggi balkon dari permukaan lantai bawah adalah 4 m, dan jarak Katrin dan Lusi adalah √40 m (6,32 m)
a. Tunjukkan bahwa segitiga KLM adalah segitiga siku-siku! b. Sudut manakah yang merupakan sudut siku-siku?
Jawaban
1. a). 11²=9²+6²
121=81+36
121=117
121>117
Karena a²>b²+c², maka segitiga tumpul
b). 12²=7²+10²
144=49+100
144=149
144<149
Karena a²<b²+c², maka segitiga lancip
c). 20²=12²+16²
400=144+256
400=400
Karena a²=b²+c², maka segitiga siku-siku
d). 13²=8²+11²
169=64+121
169=185
169<189
Karena a²<b²+c², maka segitiga lancip
e). 17²=9²+14²
289=81+196
289=277
289>277
Karena a²>b²+c², maka segitiga tumpul
f). √29=2²+5²
√29=4+25
√29=√29
Karena a²=b²+c², maka segitiga siku-siku
g). 14²=7²+12²
196=49+144
196=193
196>193
Karena a²>b²+c², maka segitiga tumpul
2. a). 13²7²+9²
169=49+81
169=130
Karena 7²+9²≠13², maka 7,9, dan 13 bukan tripel pythagoras
b). 17²=8²+15²
289=64+225
289=289
Karena 8²+15²=17², maka 8,15, dan 17 adalah triple pythagoras
c). 29²=20²+21²
841=400+441
841=841
Karena 20²+21²=29, maka 20,21, dan 29 adalah triple pythagoras
d). 6½²=6²+2½²
42,25=36+6,25
42,25=42,25
Karena 6²+2½²=6½², maka 6,2½, dan 6½ adalah tripel pythagoras
e). 13²=5²+12²
169=25+144
169=169
Karena 5²+12²=13², maka 5²,12², dan 13² adalah tripel pythagoras
f). 25²=24²+17²
625=576+289
625=865
Karena 24²+17²=25², maka 24,17, dan 25 bukan tripel pythagoras
g). 37²=12²+35²
1369=144+1225
1369=1369
Karena 12²+35²=37², maka 12,35, dan 37 adalah tripel pythagoras
h). 9²=5²+√34
81=25+√34
81=59
Karena 5²+√34=9², maka 5,√34, dan 9 bukan tripel pythagoras
3. a). AC²=AD²+CD²
AC²=9²+12²
AC²=81+144
AC²=225
AC=√225
AC=15
b). BC²=CD²+BD²
BC²=12²+16²
BC²=144+256
BC²=400
BC=√400
BC=20
AB²=AD²+BD
AB²=9²+16²
AB²=25
AB=√25
AB=5
AB²=AC²+BC²
25²=15²+20²
625=225+400
625=625
Karena a²=b²+c², maka segitiga ABC adalah segitiga siku-siku
4. a). PQ²=QS²+PS²
PQ²=16²+8²
PQ²=256+64
PQ²=320
PQ=√320
PQ=8√5
b). QR=RS+QS= 4+16=20
PR=QR-PQ²
PR²=20²-8√5²
PR²=400-320
PR²=80
PR=√80
PR=4√5
C). QR²=PQ²+PR²
20²=8√5²+4√5²
400-320+80
400=400
QR=P
Karena a²=b²+c², maka segitiga PQR adalah segitiga siku-siku di P
5. a). AB²=AC²+BC²
AB²=24²+BC²
AB²=576+100
AB²=676
AB=√676
AB=26
PA²=AC²+PC²
PA²=24²+18²
PA²=576+324
PA²=900
PA-√900
PA=30
PB²=BC²+PC²
PB²=10²+18²
PB²=100+324
PB²=424
PB=√424
PB=20,6
PA²=AB²+PB²
30²=26²+20,6²
900=1100
900<1100
Karena a²<b²+c², maka segitga lancip
6. a. Diagonal AC dan BD berpotongan tegak lurus karena diagonal AC dan BD saling berimpitan (seperti x)
b. Berbentuk bangun layang-layang
49=9+40
49=49
Karena a²=b²+c², maka segitiga siku-siku
b). Sudut L
8. LN²=MN²-LM²
LN²=17²-9²
LN²=289-81
LN²=205
LN=√205
LN=14,3
MN²=LN²+LM²
17²=9²+14,3²
289=81+205
289=286
289>286
Karena a²>b²+c², maka segitiga LMN adalah segitiga tumpul
Demikianlah soal dan kunci jawaban latihan 3 dari bab 6 pelajaran Matematika semester 2. Ingatlah untuk selalu menyukai matematika agar bisa pintar matematika. Semoga jawaban yang admin posting bermanfaat dan mudah dipahami.
Sumber buku: Matematika untuk SMP/MTs kelas viii semester 2 kurikulum 2013 revisi. Penerbit Erlangga






Post a Comment