Sebelum belajar mengenai Persamaan garis lurus kita harus mengingat konsep bahwa jika y di sebelah kiri saat dipindahkan ke kanan maka menjadi minus y. Jika nilai y diselah kiri dikali saat dipindahkan ke kanan maka menjadi dibagi. Jika y di sebelah kiri ditambah saat dipindahkan ke kanan maka menjadi dikurang. Begitupun sebaliknya
Latihan 1 halaman 120
1. Dari persamaan-persamaan berikut, manakah yang merupakan persamaan garis lurus?
a. Y=5x+2
b. 4x/y=12
c. 2x-3y=6
d. x/3+5y=1
e. 3x+12=0
f. 4x-xy=8
g. 6x-5y=2x
h. 3x/4+y/x=10
2. Gambarkan garis-garis dengan persamaan berikut terlebih dahulu membuat tabel!
a. Y=2x
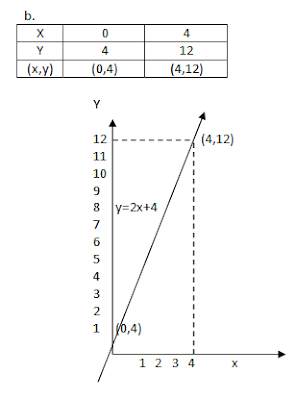
b. Y=2x+4
c. Y=-3x
d. Y=-3x+1
e. Y=2/3x+2
f. Y=2/3x+4
g. Y=-2/3x-3
h. Y=-3/4x-1
i. Y=2½x-3
j. Y=2½x+5
3. Gambarlah garis-garis dengan persamaan berikut dengan lebih dahulu menentukan nilai x jika y=0, dan nilai y jika x=0!
4. Diantara persamaan garis 3x+4y=12, 3x+4y=-12, 4x-3y=12, 4x-3y=-12, manakah yang sesuai dengan grafik berikut
5. a.Gambarlah garis dengan persamaan 2x+4y=12!
b.Jika titik P(a,5) terletak pada garis yang telah kamu buat, berapakah nilai a?
6. Periksalah, di antara titik (6,-5) dan (-4,-1), manakah yang terletak pada garis dengan persamaan berikut?
a. y=½x-8
b. y=2x+7
c. y=-1½x+4
d. 3x+2y=8
Jawab
1.a. Y=5x+2 benar garis lurus karena y=mx+c
b. 4x/y=12
4x=12y benar garis lurus karena y=mx
c. 2x-3y=6
-3y=-2x+6 benar garis lurus karena y=mx+c
d. x/3+5y=1
x/3-1=-5y
x-1=-5y(3)
x-1=-15y benar garis lurus karena y=mx+c
e. 3x+12=0 bukan garis lurus
f. 4x-xy=8 bukan garis lurus
g.6x-5y=2x
6x-2x-5y=0
4x-5y=0
4x=5y benar garis lurus karena y=mx
h.3x/4+y/x=10
3x²/4x+4y/4x=0
3x²+4y=4x bukan garis lurus
2. y=2x
y=0
0=2x
0/2=x
0=x (0,0)
X=0
Y=2(0)
Y=0 (0,0)
y=2x+4
x=0
y=2(0)+4
y=0+4
y=4 (0,4)
x=4
y=2(4)+4
y=8+4
y=12 (4,12)
Y=-3x
Y=0
0=-3x
0/3=x
0=x (0,0)
X=0
Y=-3.0
Y=0 (0,0)
y=-3x+1
x=0
Y=-3(0)+1
Y=0+1
Y=1 (0,1)
X=1
Y=-3(1)+1
Y=-3+1
Y=-2 (1,-2)
Y=2/3x+2
X=0
Y=2/3(0)+2
Y=0+2
Y=2 (0,2)
X=2
Y=2/3(2)+2
Y=4/3+2
Y=4/3+6/3
Y=10/3
Y=3⅓ (2,3⅓)
Y=2/3x+4
X=0
Y=2/3(0)+4
Y=0+4
Y=4 (0,4)
X=4
Y=2/3(4)+4
Y=8/3+4
Y=8/3+12/3
Y=20/3
Y=6⅔ (4,6⅔)
Y=-3/4x+3
X=0
Y=-3/4(0)+3
Y=0+3
Y=3 (0,3)
X=3
Y=-3/4(3)+3
Y=-9/4+3
Y=-9/4+12/4
Y=3/4 (0)+3
Y=0+3
Y=3
Y=-3/4(3)+3
Y=-9/4+3
Y=-9/4+12/4
Y=3/4 (3,3/4)
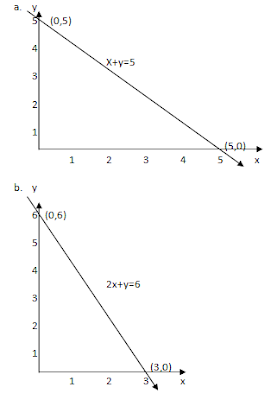
3. x+y=5
Y=0
X+0=5
X=5 (5,0)
X=0
0+y=5
Y=5 (0,5)
y=0
2x+0=6
2x=6
X=6/2
X=3 (3,0)
X=0
2.0+y=6
0+y=6
Y=6 (0,6)
2x-3y=12
Y=0
2x-3(0)=12
2x-0=12
2x=12
X=12/2
X=6 (6,0)
X=0
2(0)-3y=12
0-3y=12
-3y=12
Y=12/-3
Y=-4 (0,-3)
5x=2y=10
Y=0
5x-2(0)=10
5x-0=10
5x=10
X=10/5
X=2 (2,0)
X=0
5(0)-2y=10
0-2y=10
-2y=10
Y=10/-2
Y=-5 (0,-5)
Y=0
4x+3(0)-12=0
4x+0-12=0
4x-12=0
4x=12
X=12/4
X=3 (3,0)
X=0
4(0)+y-12=0
0+y-12=0
y-12=0
y=12 (0,12)
4. a. (3,0) dan (0,-4)
b. (0,3) dan (4,0)
c. (0,4) dan (-3,0)
d. (0,-3) dan (-4,0)
3x+4y=12
X=0
3(0)+4y=12
0+4y=12
4y=12
Y=12/4
Y =3 (0,3)
Y=0
3x+4(0)=12
3x+0=12
3x=12
X=12/3
X=4 (4,0) grafik b
4x-3y=12
X=0
4(0)-3y=12
0-3y=12
-3y=12
Y=12/-3
Y=-4 (0,-4)
Y=0
4x-3(0)=12
4x-0=12
4x=12
X=12/4
X=3 (3,0) grafik a
3x+4y=-12
X=0
3(0)+4y=-12
0+4y=-12
4y=-12
Y=-12/4
Y=-3 (0,-3)
Y=0
3x+4(0)=-12
3x+0=-12
3x=-12
X=-12/3
X=4 (-4,0) grafik d
4x=3y=-12
X=0
4(0)-3y=-12
0-3y=-12
-3y=-12
Y=-12/-3
Y=4 (0,4)
Y=0
4x=3(0)=-12
4x-0=-12
4x=-12
X=-12/4
X=-3 (-3,0) grafik c
5.a
2(0)+4y=12
0+4y=12
4y=12
Y=12/4
Y=3 (0,3)
Y=0
2x+4(0)=12
2x+0=12
2x=12
X=12/2
X=6 (6,0)
2x+4(5(=12
2x+20=12
2x=12=20
2x=-8
X=-8/2
X=-4
a =-4
6. a.X=6
Y=½(6)-8
Y=6/8-8
Y=3-8
Y=-5 (6,-5)
b. x=6
y=2(6)+7
y=12+7
y=19 (6,19)
x=-4
y=2x+7
y=2(-4)+7
y=-8+7
y=-1 (-4,-1)
c. x=6
y=-1½x+4
y=-1½(6)+4
y=-3/2(6)+4
y=-18/2+4
y=-9+4
y=-5 (6,-5)
d. x=6
3x+2y=8
3(6)+2y=8
18+2y=8
2y=8-18
Y=-10/2
Y=-5 (6,-5)
Latihan 2 halaman 126-127
1. Gambar berikut adalah tampak samping sebuah tangga beton. Hitunglah gradien tangga
7. Hitunglah nilai b, jika garis yang menghubungkan titik (3b,7) dan (-11,5b) bergradien -3!
8. Dikethaui koordinat titik A(3,-2), B(7,4), dan C(9,7)
a. Hitunglah mAB. mBC dan mAC! Bagaimana nilai ketiga gradien garis tersebut?
b. Apa yang dapat kamu simpulkan tentang ketiga titik tersebut?
a. Jika mDE=mFG, tentukan nilai p!
b. Hitunglah nilai mDE dan mFG!
c. Berbentuk bangun apakah DEFG?
Jawaban
1. Gradien tangga=perubahan nilai y/perubahan nilai x=5/10=½
2. a.Gambar 1 karena kemiringannya paling besar, semakin besar gradien semakin membahayakan.
b.Gradien tangga=perubahan nilai y/perubahan nilai x
Gradien gambar 1=5/2=2,5
Gadien gambar 2=5/3=1,8
Gradien gambar 3=5/3,5=1,4
3. a. Gradien= perubahan nilai y/perubahan nilai x
Gradien OA=4/4=1
Gradien OB= 4/6=⅔
Gradien OC= -3/4
Gradien OD=-4/-2=2
Gradien OE=-4/-5=⅘
b. Titik PQ (-1,-4) dan (7,-4)
Titik RS (7,3) dan (7,-2)
Gradien=y₂-y₁/x₂-x₁
Gradien PQ= -4-(-4)/7-(-1)=-4+4/7+1=0/8=0
Gradien RS= -2-(-3)/7-7=-5/0=0
Positif OA, OB, OC
4. Gradien=y₂-y₁/x₂-x₁
a.Gradien AB= 16-7/5-8= -9/3=-3
b.Gradien CD= -10-14/8-(-4)= -10-14/8+4= -24/12= -2
c.Gradien EF= -9-(-9)/-11-7= -9+9/= -10-7=0/-17= 0
d.Gradien PQ= 14-(-10)/-21-(-12)= 14+10/-21+12= 24/-9= -8/3= 2⅔
5. Gradien= perubahan nilai y/perubahan nilai x
Gradien AB=-3/10
Gradien BC= 6/3=2
Gradien AC=3/7
6.Gradien=y₂-y₁/x₂-x₁= 3-(-9)/2a-5a= 3+9/2a-5a= 12/-3a
masukkan nilai gradien 2
-3ax2=12
-6a=12
a =12/-6
a =-2
7.Gradien= y₂-y₁/x₂-x₁=5b-7/-11-3b
-3=-5b-7/-11-3b
(-11-3b)-3=5b-7
33+9b=5b-7
9b=5b-7-33
9b=5b-40
9b-5b=-40
4b=-40
b=-40/4
b=-10
8.m= y₂-y₁/x₂-x₁
mAB=4-(-2)/7-3=4+2/7-3=6/4=3/2=1½
mBC= 7-4/9-7=3/2=1½
mAC=7-(-2)/9-3=7+2/9-3=9/6=3/2=1½
b.Ternyata diperoleh hasil yang sama
9.Gradien PQ=gradien QR
y₁-y₂/x₁-x₂= y₁-y₃/x₁-x₃
-4-2/7-a=-4-6/7-(-8)
-6/7-a=-10/7+8
-6/7-a=-10/15
15(-6)=-10(7-a)
-90=-70+10a
-90+70=10a
-20=10a
-20/10=a
-2=a
10.a. mDE=mFG
y₂-y₁/x₂-x₁= y₂-y₁/x₂-x₁
2-6/8-p=3-(-1)/-2p-p
4/8-p=3+1/-3p
-4/8-p=4/-3p
4(-3p)=4 (8-p)
-10p=32-4p
-10+4p=32
-6p=32
P=32/-6
p =-5⅓
b.p=-5⅓)
-2p=-2(-5⅓) =10⅓
mFG=3-(-1)/10⅓-(-5⅓)= 3+1/10⅓+5⅓= 4/(31/3+16/3)= 4/47/3= 4:47/3= 4x3/47= 12/47
Latihan 3 halaman 130
1. Garis q bergradien 3½. Tentukan gradien garis jika, garis tersebut:
a. Sejajar dengan garis q
b. Tegak lurus dengan garis q
2. Garis p bergradien -4.tentukan gradien garis lain, jika garis tersebut:
a. Sejajar dengan garis p
b. Tegak lurus dengan garis p
3. a.Hitunglah gradien PQ, jika P(-6,8) dan Q(4,-7)
b.Jika garis k tegak lurus dengan PQ, tentukan gradien garis k!
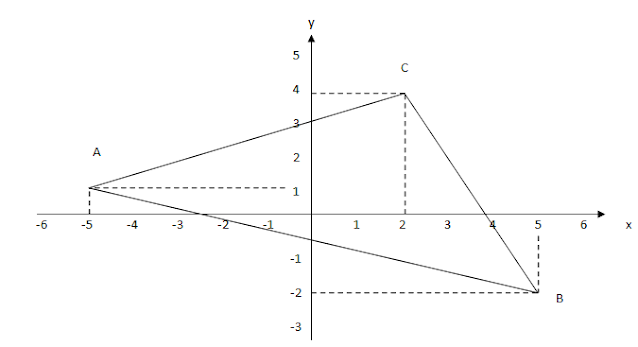
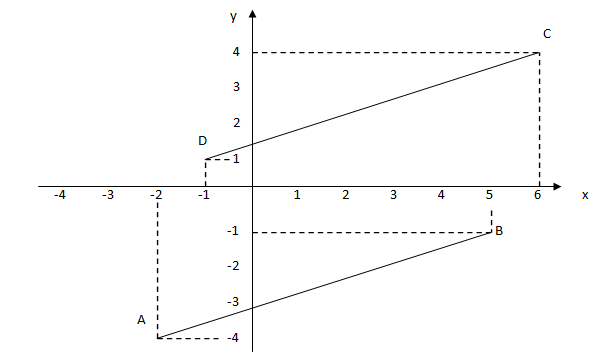
4. Gambarlah titik-titik A(-2,-4), B(5,-1), C(6,4), dan D(-1,1)
a. Tentukan gredien garis AB dan CD! Bagaimana posisi atau kemiringan garis AB dan CD?
b. Bagaimana panjang AB dan CD?
c. Mengapa dapat dikatakan bahwa ABCD berbentuk jajargenjang?
5. Perhatikan gambar berikut!Pada gambar di atas, garis g//AB dan garis tegak lurus dengan AB
a. Hitunglah gradien garis AB!
b. Tentukan gradien garis g dan k!
Jawaban
1. a.3⅓
b.mgxmh=-1
3⅓xmh=-1
7/2xmh=-1
mh=-1x2/7
mh=-2/7
2. a. -4
b.mpxmq=-1
-4xmq=-1
mq=-1/-4
mq = ¼
3. a.mPQ = y₂-y₁/x₂-x₁= -7-(8)/4-(-6)= -7-8/4+6=-15/10= -3/2= -1½
b.mPQxmk=-1
-1½xmk=-1
-3/2xmk=-1
mk=-1x-2/3
mk =⅔
4. a.mAB = y₂-y₁/x₂-x₁= -1-(-4)/5-(-2)=-1+4/5+2= 5/7
mCD = y₂-y₁/x₂-x₁= 1-4/-1-6= -3/-5= ⅗
a. Panjang AB dan CD sama
b. Karena mempunyai panjang yang sama dan membentuk jajargenjang
b.g sejajar dengan AB
g=⅔
mABxmk=-1
⅔xmk=-1
mk=-1:⅔
mk=-1x3/2
mk=-3/2
Sumber buku: Matematika untuk SMP/MTs kelas viii semester 1 kurikulum 2013 revisi. Penerbit Erlangga











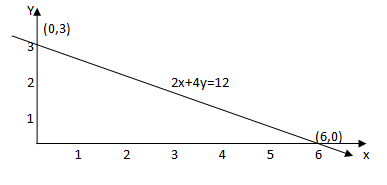






Post a Comment